Квадратные уравнения.Решение квадратных уравнений
Основные определения, формулы, теоремы
Квадратным уравнением называется уравнение вида

,
где x - переменная, a, b, c - некоторые действительные числа, причем a не равно 0.
Числа a, b и c - коэффициенты квадратного уравнения. Число a называют первым коэффициентом, b - вторым коэффициентом и c - свободным членом.
Дискриминантом квадратного уравнения 
называется действительное число

.
Теорема 1:
Если дискриминант D квадратного уравнения

, положительный, то оно имеет два различных действительных корня:
Теорема 2:
Если дискриминант D квадратного уравнения

равен нулю, то оно имеет два равных корня:
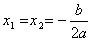

Теорема 3:
Если дискриминант D квадратного уравнения

отрицателен, то не имеет корней.
Алгоритм решения квадратного уравнения
Чтобы решить квадратное уравнение, достаточно:
1) вычислить дискриминант и сравнить его с нулем;
2) если дискриминант положителен или равен нулю, то воспользоваться формулами (*) и (**) ,соответственно, для вычисления корней
3) если дискриминант отрицательный, то записать, что корней нет.
Примечание:
Если в уравнении

дискриминант неотрицателен и второй коэффициент b - число вида 2к, где ,

, то формула корней принимает более удобный для вычисления вид:

.
Приведенные квадратные уравнения
Квадратное уравнение с коэффициентом при х2, равным 1, называется
приведенным.В общем виде приведенное квадратное уравнение обычно записывают в виде
где p и q–некоторые действительные числа.
Теорема Виета:
Если квадратное уравнение

имеет действительные корни x1и x2, то их сумма равна

, а произведение равно

.
Теорема (обратная теореме Виета): Если числа x1 и x2 таковы, что их сумма равна

,а произведение

, то эти числа являются корнями уравнения

.
Страничка Ульяновой Ю.В.
Страничка 113524
 ,
, ,
, называется действительное число
называется действительное число  .
. , положительный, то оно имеет два различных действительных корня:
, положительный, то оно имеет два различных действительных корня:


 равен нулю, то оно имеет два равных корня:
равен нулю, то оно имеет два равных корня:
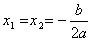
 отрицателен, то не имеет корней.
отрицателен, то не имеет корней. дискриминант неотрицателен и второй коэффициент b - число вида 2к, где ,
дискриминант неотрицателен и второй коэффициент b - число вида 2к, где ,  , то формула корней принимает более удобный для вычисления вид:
, то формула корней принимает более удобный для вычисления вид: .
.
 имеет действительные корни x1и x2, то их сумма равна
имеет действительные корни x1и x2, то их сумма равна
 , а произведение равно
, а произведение равно  .
. ,а произведение
,а произведение  , то эти числа являются корнями уравнения
, то эти числа являются корнями уравнения
 .
.